Irisan Kerucut

Irisan kerucut adalah irisan sebuah kerucut dengan sebuah bidang yang membentuk kurva dua-dimensi. Jenis kurva yang dapat terbentuk adalah lingkaran, parabola, elips, dan hiperbola.

irisan kerucut parabola elips hiperbola

Lihat juga materi StudioBelajar.com lainnya:
Persamaan dan Pertidaksamaan Logaritma
Dimensi Tiga

Lingkaran

Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama, yang disebut jari-jari lingkaran, ketitik tertentu yang disebut pusat lingkaran. Persamaan umum pada lingkaran sebagai berikut :

$x^2 + y^2 + Ax + By + c = 0$

dengan

Pusat lingkaran $(-\frac{1}{2}A, -\frac{1}{2}B)$
Jari-jari $\sqrt{\frac{1}{4}A^2 + \frac{1}{4}B^2 - C}$

Persamaan lingkaran jika titik pusatnya diketahui:

irisan kerucut lingkaran

Posisi titik $P(x_1,x_2)$ terhadap lingkaran dengan persamaan $(x - a)^2 + (y - b)^2 = r^2$ adalah:

P di dalam lingkaran jika $(x_1 - a)^2 + (y_1 - b)^2 < r^2$
P di lingkaran jika $(x_1 - a)^2 + (y_1 - b)^2 = r^2$
P di luar lingkaran jika $(x_1 - a)^2 + (y_1 - b)^2 > r^2$

posisi titik di dalam lingkaran

Posisi titik $P{x_1,x2}$ terhadap lingkaran dengan persamaan $x^2 + y^2 + Ax + By + C = 0$ ditentukan dengan Kuasa K, dimana $K = x_1^2 + y_1^2 + Ax_1 + By_1 + C$ .

P di dalam lingkaran jika $K < r^2$
P di lingkaran jika $K = r^2$
P di luar lingkaran jika $K > r^2$

Posisi garis $y = mx + n$ terhadap lingkaran $x^2 + y^2 + Ax + By + C = 0$ memiliki tiga kemungkinan titik potong. Hal ini ditentukan oleh diskriminan $D = b^2 - 4ac$ dari persamaan kuadrat sekutu antara garis dan lingkaran. Sehingga:

$D > 0$ , garis memotong lingkaran di dua titik
$D = 0$ , garis menyinggung lingkaran di satu titik
$D < 0$ , garis tidak memotong lingkaran.

posisi garis terhadap lingkaran

Garis singgung yang melewati titik singgung $(x_1,y_1)$ dapat ditentukan persamaan garisnya dengan cara:

garis singgung yang melewati lingkaran

Persamaan garis singgung dengan gradien m yang menyinggung lingkaran dapat ditentukan dengan cara:

persamaan garis singgung lingkaran dengan gradien m

Garis singgung dengan gradien m akan sejajar dengan garis h $(y = mx_h + n)$ jika $m = m_h$
Garis singgung dengan gradien m akan tegak lurus dengan garis h $(y = mx_h + n)$ jika $m = \frac{1}{m_h}$

Parabola

Parabola adalah tempat kedudukan titik-titik yang jaraknya terhadap titik tertentu, yang dinamakan titik fokus (f), dan garis tertentu, yang dinamakan direktriks (d), selalu sama. (karena e = 1)

irisan kerucut parabola

Berikut adalah macam-macam persamaan parabola:

Titik Puncak	Titik Fokus	Persamaan Parabola	Keterangan
$(0,0)$	$(p,0)$	$y^2 =4px$	Kurva terbuka kekanan Persamaan direktriks: $x = -p$ Sumbu simetri: $y = 0$ Panjang latus rectum $= 4p$
	$(-p,0)$	$y^2 = -4px$	Kurva terbuka kekiri Persamaan direktriks: $x =p$ Sumbu simetri: $y = 0$ Panjang latus rectum $=4p$
	$(0,p)$	$x^2 = 4py$	Kurva terbuka keatas Persamaan direktriks: $y = -p$ Sumbu simetri: $x = 0$ Panjang latus rectum
	$(0,-p)$	$x^2 = -4py$	Kurva terbuka keatas Persamaan direktriks: $y = p$ Sumbu simetri: $x = 0$ Panjang latus rectum
$(a,b)$	$(a + p,0)$	$(y-b)^2 = 4p(x - a)$	Kurva terbuka kekanan Persamaan direktriks: $x = a-p$ Sumbu simetri: $y = b$ Panjang latus rectum $=4p$
	$(a - p,0)$	$(y - b)^2 = -4p(x - a)$	Kurva terbuka kekiri Persamaan direktriks: $x = a + p$ Sumbu simetri: $y = b$ Panjang latus rectum $= 4p$
	$(0,a + p)$	$x - a^2 = 4p(y - b)$	Kurva terbuka keatas Persamaan direktriks: $y = b - p$ Sumbu simetri: $x = a$ Panjang latus rectum $= 4p$
	$(0,a - p)$	$x - a^2 = -4p(y - b)$	Kurva terbuka keatas Persamaan direktriks: $y = b + p$ Sumbu simetri: $x = a$ Panjang latus rectum $= 4p$

Persamaan garis singgung parabola yang melalui titik singgung $(x_1,y_1)$ pada parabola adalah:

persamaan parabola

Persamaan garis singgung parabola dengan gradien m pada parabola adalah:

persamaan garis singgung parabola dengan gradien m

Elips

Elips didefinisikan sebagai kedudukan titik-titik yang jumlah jaraknya dari dua titik (titik fokus) adalah konstan.

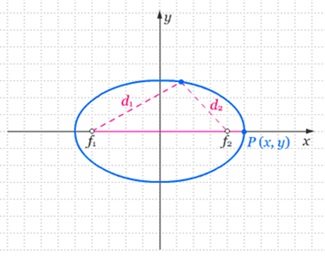
irisan kerucut elips

Bentuk persamaannya sebagai berikut:

Pusat

Puncak Sumbu Mayor

Puncak Sumbu Minor

Persamaan Elips

$(0,0)$

$A_1(-a,0)$

$A_2(a,0)$

$B_1(0,-b)$

$B_2(0,b)$

$\frac{x^2}{a^2} + \frac{y^2}{b^2}=1$

Kurva lonjong mendatar
Panjang sumbu mayor (sumbu panjang) $=2a$
Panjang sumbu minor (sumbu pendek) $= 2b$
$a > b \rightarrow c^2 = a^2 - b^2$
Titik focus $f_1 (-c,0)$ dan $f_2(c,0)$
Eksentrisitas $e = \frac{c}{a}$
Direktriks $x = -\frac{a^2}{c}$ dan $x = \frac{a^2}{c}$
Panjang latus rectum $= \frac{2b^2}{a}$

$A_1(0,-a)$

$A_2(0,a)$

$B_1(-b,0)$

$B_2(b,0)$

$\frac{x^2}{b^2} + \frac{y^2}{a^2}=1$

Kurva lonjong vertikal
Panjang sumbu mayor (sumbu panjang) $=2a$
Panjang sumbu minor (sumbu pendek) $=2b$
$a > b \rightarrow c^2 = a^2 - b^2$
Titik focus $f_1(0,-c)$ dan $f_2(0,c)$
Eksentrisitas $e = \frac{c}{d}$
Direktriks $x =-\frac{a^2}{c}$ dan $x =\frac{a^2}{c}$
Panjang latus rectum $=\frac{2b^2}{a}$

$(h,k)$

$A_1(h-k,a)$

$A_2(h+a,0)$

$B_1(h,k-b)$

$B_2(h,k+b)$

$\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1$

Kurva lonjong mendatar
Panjang sumbu mayor (sumbu panjang) $=2a$
Panjang sumbu minor (sumbu pendek) $=2b$
$a > b \rightarrow c^2 = a^2 -b^2$
Titik focus $f_1(h-c,0)$ dan $f_2(h+c,0)$
Eksentrisitas $e = \frac{c}{d}$
Direktriks $x = h -\frac{a^2}{c}$ dan $x = h + \frac{a^2}{c}$
Panjang latus rectum $= \frac{2b^2}{a}$

$A_1(h,k - a)$

$A_2(h,k + a)$

$B_1(h - b,k)$

$B_2(h + b,k)$

$\frac{(x-h)^2}{b^2} + \frac{(y-k)^2}{a^2} = 1$

Kurva lonjong vertikal
Panjang sumbu mayor (sumbu panjang) $=2a$
Panjang sumbu minor (sumbu pendek) $=2b$
$a > b \rightarrow c^2 = a^2 - b^2$
Titik focus $f_1(0,k - c)$ dan $f_2(0,k + c)$
Eksentrisitas $e = \frac{c}{a}$
Direktriks $x = k - \frac{a^2}{c}$ dan $x = k + \frac{a^2}{c}$
Panjang latus rectum $= \frac{2ab^2}{a}$

Dengan persamaan garis singgung yang melewati titik $(x_1,y_1)$ pada elips adalah:

persamaan elips

Persamaan garis singgung parabola dengan gradien m pada elips adalah:

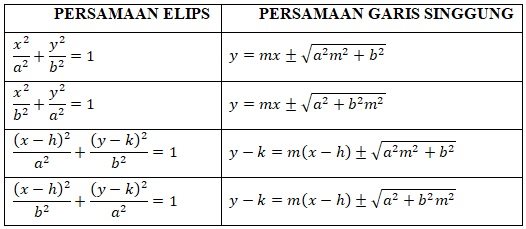
persamaan garis singgung elips dengan gradien m

Hiperbola

Hiperbola didefinisikan sebagai kedudukan titik-titik yang selisih jaraknya dari dua titik (titik fokus) adalah konstan.

irisan kerucut hiperbola

Persamaan hiperbola dengan titik pusat $(0,0)$ dan $(h,k)$ sebagai berikut:

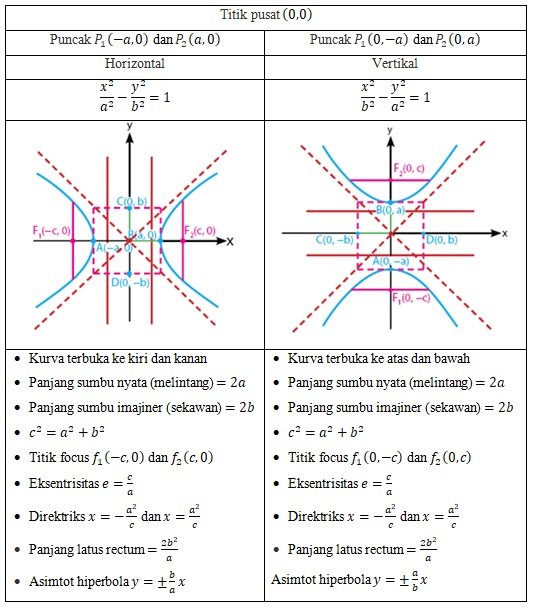
persamaan hiperbola dengan titik pusat 00

persamaan hiperbola dengan titik pusat h k

Persamaan garis singgung hiperbola yang melalui titik $(x_1,y_1)$ adalah:

persamaan hiperbola melalui titik x1 y1

Persamaan garis singgung hiperbola dengan gradien m pada elips adalah:

persamaan garis singgung hiperbola dengan gradien m

Contoh Soal Irisan kerucut dan Pembahasan

Contoh Soal Irisan Kerucut 1

Lingkaran $(x + 1)^2 + (y - 3)^2 = 9$ memotong garis $y = 3$ . Garis singgung yang melalui titik potong antara lingkaran dan garis tersebut adalah? (UN 2012)