Dinamika Rotasi

Dinamika Rotasi – Pengantar

Ketika suatu benda bergerak pada lintasan lurus, maka benda tersebut dapat dikatakan bergerak secara translasi. Akan tetapi, ketika benda tersebut bergerak pada sumbu putarnya atau bergerak pada lintasan melingkar, maka benda tersebut bergerak secara rotasi.

Lihat juga materi StudioBelajar.com lainnya:
Efek Doppler
Fluida Statis

Ketika benda bergerak secara translasi, benda tersebut dapat menerima gaya eksternal jika diberikan. Gaya yang diberikan ini dapat mengubah arah lintasan benda. Akan tetapi ketika benda bergerak berputar atau pada lintasan melingkar, benda tersebut dapat pula menerima gaya yang lebih dikenal sebagai Torsi.

Momen Gaya atau Torsi

Momen gaya atau torsi dapat didefinisikan dengan beberapa pengertian:

Torsi adalah gaya pada sumbu putar yang dapat menyebabkan benda bergerak melingkar atau berputar.
Torsi disebut juga momen gaya.
Momen gaya/torsi benilai positif untuk gaya yang menyebabkan benda bergerak melingkar atau berputar searah dengan putaran jam (clockwise), dan jika benda berotasi dengan arah berlawanan putaran jam (counterclockwise), maka torsi penyebabnya bernilai negatif.
Setiap gaya yang arahnya tidak berpusat pada sumbu putar benda atau titik massa benda dapat dikatakan memberikan Torsi pada benda tersebut.

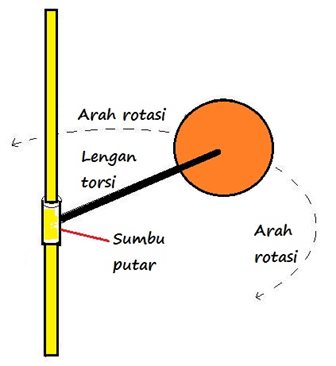
torsi pada dinamika rotasi

Torsi atau momen gaya dirumuskan dengan:

$\tau = r \times F$

dimana:
$\tau$ adalah torsi atau momen gaya (Nm)
r adalah lengan gaya (m)
F adalah gaya yang diberikan tegak lurus dengan lengan gaya (N)

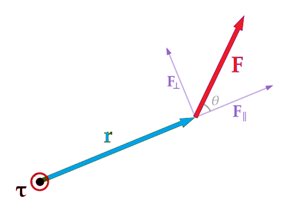
Jika gaya yang bekerja pada lengan gaya tidak tegak lurus, maka besar torsinya adalah:

$\tau = r \times F \times \sin \theta$

dimana $\theta$ adalah sudut antara gaya dengan lengan gaya.

rumus torsi

Yuk belajar materi ini juga:
Induksi Matematika
Senyawa Hidrokarbon
Struktur Sel

Momen Inersia

Konsep momen inersia pertama kali diberikan oleh Leonhard Euler. Momen inersia didefinisikan sebagai kelembaman suatu benda untuk berputar pada porosnya, atau dapat dikatakan ukuran kesukaran untuk membuat benda berputar atau bergerak melingkar. Besar momen inersia bergantung pada bentuk benda dan posisi sumbu putar benda tersebut.

momen inersia dengan sumbu putarnya

Momen inersia dirumuskan dengan:

$I = mr^2$

dimana:
I adalah momen inersia (kgm²)
r adalah jari-jari (m)
m adalah massa benda atau partikel (kg)

Benda yang terdiri atas susunan partikel atau benda-benda penyusunnya yang lebih kecil, jika melakukan gerak rotasi, maka momen inersianya sama dengan hasil jumlah semua momem inersia penyusunnya:

$I = \Sigma m_i \times r_i^2$

$I = (mr_1^2) + (mr_2^2) + (mr_3^2) + \cdots$

Momentum Sudut

Momentum sudut adalah ukuran kesukaran benda untuk mengubah arah gerak benda yang sedang berputar atau bergerak melingkar.

Momentum sudut dirumuskan dengan:

$L = I \omega$

$L = mvr$

dimana:
L adalah momentum sudut (kgm²s^-1)
I adalah momen inersia benda (kgm²)
$\omega$ adalah kecepatan sudut benda (rad/s)
m adalah massa benda (kg)
v adalah kecepatan linear (m/s)
r adalah jarak benda ke sumbu putarnya (m)

Energi Kinetik Rotasi

Energi kinetik rotasi adalah energi kinetik yang dimiliki oleh benda yang bergerak rotasi yang dirumuskan dengan:

$Ek_r = \frac{1}{2} I \omega^2$

Jika benda tersebut bergerak secara rotasi dan juga tranlasi, maka energi kinetik totalnya adalah gabungan dari energi kinetik translasi rotasi dan energi kinetik rotasi:

$Ek_t = Ek + Ek_r$

$Ek_t = \frac{1}{2} mv^2 + \frac{1}{2} I \omega^2$

dimana:
Ek_t adalah Energi kinetik total benda
Ek adalah energi kinetik translasi
Ek_r adalah energi kinetik rotasi
m adalah massa benda (kg)
v adalah kecepatan linear (m/s)
I adalah momen inersia benda (kgm²)
$\omega$ adalah kecepatan sudut benda (rad/s)

Yuk belajar materi ini juga:
Teks Prosedur
Analytical Exposition
Persamaan Trigonometri

Hukum Newton 2 Untuk Rotasi

Benda yang bergerak secara translasi menggunakan hukum newton II ( $\Sigma F = ma$ ) dan benda yang bergerak secara rotasi juga memakai konsep hukum Newton yang sama, akan tetapi besarannya memakai besaran-besaran rotasi. Sehingga, Hukum Newton II untuk benda yang bergerak secara rotasi atau bergerak melingkar memakai rumus:

$\tau = I \alpha$

dimana:
$\tau$ adalah total torsi yang bekerja pada benda
I adalah momen inersia benda
$\alpha$ adalah percepatan sudut benda

Dibawah ini adalah tabel yang menganalogikan antara gerak translasi dan gerak rotasi

Besaran-besaran Pada Gerak Translasi			Besaran-besaran pada Gerak Rotasi
Besaran	Rumus	Satuan	Besaran	Rumus	Satuan
Jarak tempuh	s	m	Jarak tempuh sudut	q = s/r	rad
Kecepatan	V = s/t	m/s	Kecepatan sudut	$\omega = V/r$	rad/s
Percepatan	a = V/t	m/s²	Percepatan sudut	$\alpha = a/r$	rad/s²
Massa	m	kg	Momen inersia	I = mr²	kg . m²
Gaya	F = ma	N	Momen gaya/torsi	$\tau = rF$	Nm
Momentum	p = mv	kg . m/s	Momentum sudut	$L = I \omega$	kg . m²/s
Energi kinetik	$Ek = \frac{1}{2} mv^2$	Nm (Joule)	Energi kinetik rotasi	$Ek = \frac{1}{2} I \omega^2$	Nm (Joule)

Dibawah ini adalah tabel yang menyimpulkan hubungan antara gerak translasi dan gerak rotasi

Konsep	Gerak Translasi	Hubungan	Gerak Rotasi
Penyebab akselerasi	$\Sigma F$	$\tau = r \times F$	$\Sigma \tau$
Kesukaran untuk berakselerasi	m	$I = \Sigma m_i \times r_i^2$	I
Hukum newton 2	$\Sigma F = ma$		$\Sigma \tau = I \alpha$

Contoh Soal Dinamika Rotasi/Momen Gaya

contoh soal dinamika rotasi momen gaya

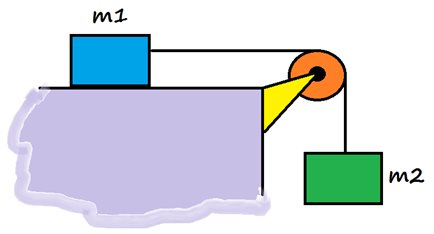
Pada gambar diatas, sebuah katrol silinder pejal ( $Ek = \frac{1}{2}m r^2$ ) dengan massa 3kg dan berjari-jari 20 cm dihubungkan dengan dua buah tali yang masing-masing memiliki terpaut pada benda bermassa dimana m₁ = 6kg dan m₂ = 3kg. Sistem diatas berada dalam kondisi tertahan diam dan kemudian dilepaskan. Jika tidak terjadi gesekan pada lantai dengan, berapakah percepatan kedua benda tersebut?