Fungsi dalam Matematika: Pengertian, Relasi, Fungsi Komposisi, Fungsi Invers, dan Contoh Soal
Penjelasan tentang Relasi dan Fungsi
Pengertian Fungsi: Relasi dari himpunan A ke himpunan B disebut fungsi atau pemetaan jika dan hanya jika setiap anggota himpunan A berpasangan dengan tepat satu anggota himpunan B.
Suatu fungsi atau pemetaan dapat disajikan dalam bentuk himpunan pasangan terurut, rumus, diagram panah, atau diagram cartesius. Fungsi f yang memetakan himpunan A ke himpunan B ditulis dengan notasi:
Dengan:
- A disebut domain (daerah asal) dinotasikan
- B disebut Kodomain (daerah kawan) dinotasikan
disebut range (daerah hasil), dinotasikan dengan
Turunan Fungsi Aljabar & Trigonometri
Persamaan Garis Lurus
Sebagai contoh:
| Contoh 1 | Contoh 2 | Contoh 3 |
 |
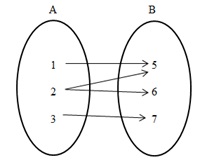 |
 |
| Bukan fungsi karena terdapat anggota di A yang tidak dihubungkan dengan anggota di B | Bukan fungsi karena terdapat anggota di A yang dihubungkan lebih dari satu dengan anggota di B | Meupakan fungsi karena setiap anggota di A tapat dihubungkan dengan satu anggota di B |
Sifat-sifat Fungsi
- Fungsi surjektif
Pada fungsi , jika setiap elemen di B mempunyai pasangan di A atau
, atau setiap
terdapat
sedemikian sehingga
. Contoh:

- Fungsi Into
Pada fungsi , jika terdapat elemen di B yang tidak mempunyai pasangan di A.
Contoh:

- Fungsi Injektif
Pada fungsi , jika setiap elemen di B mempunyai pasangan tepat satu elemen dari A.
Contoh:

- Fungsi Bijektif
Jika fungsi merupakan fungsi surjektif sekaligus fungsi injektif.
Contoh:

Fungsi Komposisi
Fungsi komposisi merupakan susunan dari beberapa fungsi yang terhubung dan bekerja sama.
Sebagai ilustrasi jika fungsi f dan g adalah mesin yang bekerja beriringan. Fungsi f menerima input berupa (x) yang akan diolah di mesin f dan menghasilkan output berupa . Kemudian
dijadikan input untuk diproses di mesin g sehingga didapat output berupa
.
Ilustrasi tersebut jika dibuat dalam fungsi merupakan komposisi g dan f yang dinyatakan dengan sehingga:
dengan syarat: .

Komposisi bisa lebih dari dua fungsi jika ,
, dan
, maka
dan dinyatakan dengan:
Sifat-sifat fungsi komposisi:
Operasi pada fungsi komposisi tidak besifat komutatif
Operasi bersifat asosiatif:
Contoh:
Jika dan
, maka g(x) adalah
Fungsi Invers
Jika fungsi memiliki relasi dengan fungsi
, maka fungsi g merupakan invers dari f dan ditulis
atau
. Jika
dalam bentuk fungsi, maka
disebut fungsi invers.
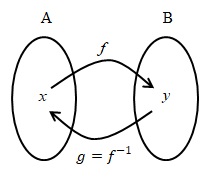
Menentukan Invers
Menentukan invers suatu fungsi dapat ditempuh dengan cara berikut:
Ubah persamaan ke dalam bentuk
Gantikan x dengan sehingga
Gantikan y dengan x sehingga diperoleh invers berupa
Contoh:
Menentukan invers dari :
Sehingga inversnya adalah
dan bukan merupakan fungsi karena memiliki dua nilai.
Rumus Fungsi Invers
Rumus Fungsi Invers
| JENIS FUNGSI | f(x) | |
| Fungsi linier | |
|
| Fungsi pecahan linier | |
|
| Fungsi Irrasional | |
|
| Fungsi eksponen | |
|
| Fungsi logaritma | |
|
Contoh
| JENIS FUNGSI | |
|
| Fungsi linier | |
|
| Fungsi pecahan linier | |
|
| Fungsi Irrasional | |
|
| Fungsi eksponen | |
|
| Fungsi logaritma | |
|
Invers dari Fungsi Komposisi
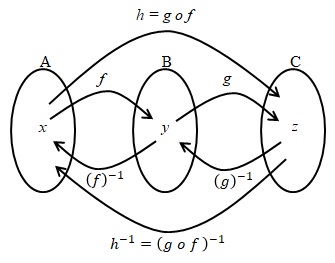
Berdasar gambar, jika f, g, h adalah fungsi dengan contoh ,
, dan
.
Jika adalah invers fungsinya yaitu
,
, dan
, maka dirumuskan beserta contohnya:
Berdasarkan rumusan tersebut, dapat diturunkan operasi komposisi fungsi sebagai berikut:
- Jika diketahui
dan
atau
, maka
- Jika diketahui
dan
atau
, maka
- Jika diketahui
,
, dan
, maka
- Jika diketahui
,
, dan
, maka
Contoh Soal Fungsi Komposisi Fungsi Invers dan Pembahasan
Contoh Soal Fungsi Komposisi
Jika dan
, tentukanlah nilai
Pembahasan
Maka:
Contoh Soal Fungsi Invers
Diketahui , tentukan
.
Pembahasan
Maka,
Contoh Soal Fungsi Komposisi Fungsi Invers
Misalkan untuk
dan
untuk
. Jika
, tentukan nilai (x)
.
Pembahasan
Maka,
Mengapa Harus Belajar Fungsi, Relasi, Fungsi Invers, dan Fungsi Komposisi?
- Fungsi: Dasar dari Semua Perhitungan
- Fungsi adalah konsep dasar yang digunakan dalam hampir semua cabang matematika. Menguasai fungsi berarti kamu bisa mengerti dan menerapkan prinsip-prinsip matematika dalam berbagai situasi, seperti menghitung bunga bank, memprediksi pertumbuhan populasi, atau bahkan dalam pemrograman komputer.
- Relasi: Memahami Hubungan Antara Hal-Hal
- Belajar tentang relasi membantu kamu mengerti bagaimana dua set atau lebih hal saling berhubungan. Ini penting, misalnya, dalam statistik saat mengkorelasikan data, atau dalam ilmu sosial untuk memahami hubungan antarvariabel.
- Fungsi Invers: Balik Arah Pemikiran
- Fungsi invers mengajarkan kamu untuk ‘membalik’ pemikiran. Dalam kehidupan nyata, ini seperti menemukan solusi dari masalah yang ada. Misalnya, kalau kamu tahu akhir dari suatu proses, bagaimana cara menemukan awal proses tersebut? Ini berguna dalam berbagai bidang, seperti kriptografi atau pemecahan masalah logis.
- Fungsi Komposisi: Menggabungkan Langkah-Langkah
- Menggabungkan dua fungsi atau lebih untuk membuat fungsi baru (komposisi) adalah skill penting. Ini mirip dengan mengikuti serangkaian instruksi untuk mencapai hasil akhir. Dalam bidang seperti komputasi, fisika, dan rekayasa, fungsi komposisi digunakan untuk memodelkan proses yang kompleks.
Belajar tentang semua ini bukan hanya tentang matematika, tapi juga tentang melatih cara berpikir kamu secara logis dan sistematis, yang nantinya sangat berguna dalam studi lanjutan dan di dunia kerja. Plus, ini juga membantu kamu mengerti lebih dalam tentang dunia di sekitar kita. Jadi, semangat belajar ya!
Kontributor: Alwin Mulyanto, S.T.
Alumni Teknik Sipil FT UI
Materi StudioBelajar.com lainnya:
