Kuartil, Desil, Simpangan Baku, Varian, dsb

Kuartil (Q)

Kuartil adalah nilai yang membagi data menjadi empat bagian yang sama banyak setelah data diurutkan dari yang terkecil hingga yang terbesar. Terdapat tiga kuartil, yaitu kuartil bawah $(Q_1)$ , kuartil tengah $(Q_2)$ atau median, dan kuartil atas $(Q_3)$ . Kuartil didapat dengan cara :

Mengurutkan data dari nilai terkecil hingga terbesar
Menentukan median atau $(Q_2)$
Menentukan $(Q_1)$ (median data kurang dari $(Q_2)$ ) dan $(Q_3)$ (median data lebih dari $(Q_2)$ )

Lihat juga materi StudioBelajar.com lainnya:
Persamaan Trigonometri
Mean Median Modus

Contoh, data yang diurutkan:

rumus cara mencari kuartil

$(Q_2) = 4$
$(Q_1) = \frac{1}{2}(2+3) = 2.5$
$(Q_3) = \frac{1}{2}(6+6) = 6$

Untuk data berkelompok, kuartil dihitung dengan rumus:

$Q_i = t_b + (\frac{\frac{i}{4}n-f_k}{f})c$

Dengan:
$t_b =$ tepi bawah kelas kuartil
$n =$ banyak data
$f_k =$ frekuensi kumulatif sebelum kelas kuartil
$f =$ frekuensi kumulatif kelas kuartil
$c =$ panjang kelas
$i =$ 1,2,3

(Contoh ada di soal 1 di bawah)

Desil

Desil adalah nilai yang membagi data menjadi sepuluh bagian yang sama banyak setelah data diurutkan dari yang terkecil hingga yang terbesar. Letak desil bisa direntukan dengan rumus:

$D_i$ terletak pada nilai ke – $\frac{i(n+1)}{10}$

Contoh, data yang diurutkan:

cara mencari dan rumus desil

$D_3$ ada di nilai ke- $\frac{i(n+1)}{10} = \frac{3(15)+1}{10} = 4.8$ , sehingga

$D_3 = x_4 + 0.8(x_5 - x_4) = 6 + 0.8(6 - 6) = 6$

$D_6$ ada di nilai ke- $\frac{i(n+1)}{10} = \frac{6(15 + 1)}{10} = 9.6$ , sehingga

$D_6 = x_9 + 0.6(x_10 - x_9) = 7 + 0.6(8 - 7) = 7.6$

Untuk data berkelompok, desil didapat dengan rumus berikut :

$D_i = t_b + (\frac{\frac{i}{10}n-f_k}{f})c$

Dengan:
$t_b =$ tepi bawah kelas desil
$n =$ banyak data
$f_k =$ frekuensi kumulatif sebelum kelas desil
$f =$ frekuensi kumulatif kelas desil
$c =$ panjang kelas
$i =$ 1,2,3,…,9

(Contoh ada di soal 1)

Jangkauan (Rentang), Hamparan, dan Simpangan Kuartil

Jangkauan data $(J)$ adalah selisih antara data terbesar dan data terkecil.

$J = x_{max}-x_{min}$

Hamparan atau jangkauan antar kuartil $(H)$ adalah selisih antara kuartil ketiga dan pertama

$H = Q_3 - Q_1$

Simpangan kuartil $Q_d$ adalah setengah kali panjang hamparan

$Q_d = \frac{1}{2}(Q_3 - Q_1)$

(Contoh di Soal 1 dan Soal 2)

Lihat juga materi StudioBelajar.com lainnya:
Medan Magnet
Benzena
Kalimat Efektif

Simpangan Rata-rata

Simpangan rata-rata $(SR)$ merupakan jarak rata-rata suatu data terhadap rataannya. Simpangan rata-rata dapat dicari dengan rumus:

$SR = \frac{1}{2} \sum \limits^N_{I=1}\mid x_i - \bar x\mid$

Dengan:
$n$ = banyak data
$x_i$ = nilai data ke-i
$\bar x$ = nilai rata-rata

(Contoh di Soal 2)

Sedangkan untuk data berkelompok, rumus simpangan rata-rata $(SR)$ adalah :

$SR = \frac{1}{n} \sum \limits^k_{i=1}f_i\mid x_i - \bar x\mid$

Dengan:

$k$ = banyak kelas
$x_i$ = titik tengah kelas ke-i
$\bar x$ = nilai rata-rata
$n$ = $\sum^k_{i=1}f_i$

(Contoh di Soal 3)

Ragam

Ragam atau varian $(S^2)$ menyatakan rata-rata kaudrat jarak suatu data terhadap rataannya. Rumus untuk mendapatkan ragam atau varian adalah:

$S^2 = \frac{1}{n} \sum \limits^n_{i=1}(x_i - \bar x)^2$

Dengan:

$n$ = banyak data
$x_i$ = nilai data ke-i
$\bar x$ = nilai rata-rata

(Contoh di Soal 2)

Sedangkan untuk Ragam atau varian $(S^2)$ untuk data berkelompok dapat ditentukan dengan rumus berikut:

$S^2 = \frac{1}{n} \sum \limits^k_{i=1}f_i(x_i - \bar x)^2$

Atau

$S^2 = \frac{1}{n} \sum \limits^k_{i=1}f_ix_i^2 - (\frac{1}{n} \sum \limits^k_{i=1}f_ix_i)^2$

Dengan:
$k$ = banyak kelas
$x_i$ = titik tengah kelas ke-i
$\bar x$ = nilai rata-rata
$n = \sum^k_{i=1}f_i$

(Contoh di Soal 3)

Rumus diatas dapat diubah dengan menggunakan simpangan rataan menjadi

$S^2 = \frac{1}{n} \sum \limits^k_{i=1}f_id_i^2 - (\frac{1}{n} \sum \limits^k_{i=1}f_id_i)^2$

Simpangan Baku

Simpangan baku atau standar deviasi $(S)$ adalah rata-rata jarak penyimpangan titik-titik data diukur dari nilai rata-rata data tersebut. Simpangan baku dapat ditentukan dengan rumus :

$S = \sqrt{S^2} = \sqrt{\frac{1}{n} \sum \limits^n_{i=1}(x_i - \bar x)^2}$

Contoh di Soal 2

Sedangkan untuk data berkelompok, Simpangan baku atau standar deviasi dapat ditentukan dengan rumus:

$S = \sqrt{S^2} = \sqrt{\frac{1}{n} \sum \limits^k_{i=1}f_i(x_i - \bar x)^2}$

Contoh di Soal 3

Contoh Soal Kuartil, Simpangan Kuartil, Simpangan Baku, dsb & Pembahasan

Contoh Soal Kuartil, Simpangan Kuartil, dsb.

Tentukan nilai kuartil bawah, kuartilatas, desil ke-6, jangkauan antar kuartil, dan simpangan kuartil dari data berikut:

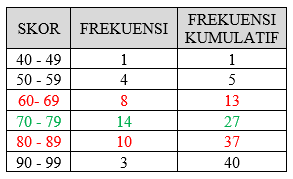
contoh soal jangkauan simpangan kuartil

Pembahasan

Panjang kelas: $c = 10$
Banyak data: $n = 40$

Maka letaknya:

Kelas $Q_1$ ada pada $x$ ke $\frac{i}{4}n = \frac{1}{4}(40) = 10$ yaitu di kelas 60 – 69
Kelas $\frac{i}{4}n = \frac{3}{4}(40) = 30$ yaitu di kelas 80 – 89
Kelas $D_6$ ada pada x $x$ $\frac{i(n+1)}{10} = \frac{6(40+1)}{10} = 24.6$ yaitu di kelas 70 – 79

Sehingga:

$Q_1 = t_b + (\frac{\frac{i}{4}n-f_k}{f})c = 59.5 + (\frac{\frac{1}{4}(40)-8}{8}) 10 = 65.75$

$Q_3 = t_b + (\frac{\frac{i}{4}n-f_k}{f})c = 79.5 + (\frac{\frac{8}{4}(40)-27}{10}) 10 = 82.5$

$D_6 = t_b + (\frac{\frac{6}{10}(40)-13}{14})10 = 77.36$

Jangkauan antar kuartil (H):

$H = Q_3 - Q_1 = 82.5 - 65.75 = 16.75$

Simpangan kuartil $Q_d$ :

$Q_d = \frac{1}{2}H = \frac{1}{2}(16.75) = 8.375$

Lihat juga materi StudioBelajar.com lainnya:
Metabolisme
Procedure Text
Teori Relativitas

Contoh Soal Simpangan Baku, Ragam, dsb.

Diketahui data 3, 4, 4, 5, 6, 7, 8, 9, 9. Tentukan nilai dari jangkauan, jangkauan antar kuartil, simpangan kuartil, simpangan rata-rata, ragam, dan simpangan baku data tersebut.

Pembahasan:

contoh soal simpangan baku

Dengan $Q_1 = 4$ , $Q_2 = 6$ , dan $Q_3 = 8.5$ , maka

Mean: $\bar x = \frac{3+4+4+5+6+7+8+9+9}{9} = \frac{55}{9} = 6.11$
Jangkauan: $(J) = x_{max} - x_{min} = 9 -3 = 6$
Jangkauan antar kuartil: $H= Q_3 - Q_1 = 8.5 - 4 = 4.5$
Simpangn kuartil: $Q_d = \frac{1}{2}(Q_3 - Q_1) = \frac{1}{2}(Q_3 - Q_1) = \frac{1}{2}(8.5 - 4) = 2.25$
Simpang rata-rata:

$SR =\frac{1}{n} \sum \limits^k_{i=1} \mid x_i - \bar x\mid$

$SR = \frac{1}{9} \sum \limits^k_{i=1} \mid 3 - 6.11\mid$ + $\mid 4 - 6.11\mid$ + $\mid 4 - 6.11\mid$ + $\mid 5 - 6.11\mid$ + $\mid 6 - 6.11\mid$ + $\mid 7 - 6.11\mid$ + $\mid 8 - 6.11\mid$ + $\mid 9 - 6.11\mid$ + $\mid 9 - 6.11\mid$

$SR=\frac{1}{9} \sum \limits^k_{i=1} \mid -3.11\mid$ + $\mid -2.11\mid$ + $\mid -2.11\mid + -1.11\mid$ + $\mid -1.11\mid$ + $\mid 0.89\mid$ + $\mid 1.89\mid$ + $\mid 2.89\mid$ + $\mid 2.89\mid$

$SR = \frac{1}{9} \times 17 = 1.89$

Ragam:

$S^2 = \frac{1}{n} \sum \limits^k_{i=1}(x_i - \bar x)^2$

$S^2 = \frac{1}{9} \sum\limits^k_{i=1}(3 - 6.11)^2$ + $(4 - 6.11)^2$ + $(5 - 6.11)^2 + (6 - 6.11)^2$ + $(7 - 6.11)^2 + (8 - 6.11)^2$ + $(9 - 6.11)^2 + (9 - 6.11)^2$

$SR = \frac{1}{9} \sum \limits^k_{i=1} (-3.11)^2$ + $(-2.11)^2$ + $(-2.11)^2$ + $(-1.11)^2$ + $(-1.11)^2$ + $(0.89)^2$ + $(1.89)^2$ + $(2.89)^2$ + $(2.89)^2$

$S^2 = \frac{1}{9} \sum \limits^k_{i=1}$ 9.6721 + 4.4521 + 4.4521 + 1.2321 + 1.2321 + 0.7921 + 3.5721 + 8.3521 + 8.3521

$S^2 = \frac{1}{9} \times 42.1089 = 4.6788$

Simpangan baku:

$S = \sqrt{S^2} = \sqrt{4.6788} = 2.163$

Contoh Soal Jangkauan, Simpangan Rata-rata, dsb.

Tentukan jangkauan, hamparan, simpangan kuartil, simpangan rata-rata, ragam, dan simpangan baku pada data berikut:

Nilai	Frekuensi
40-49	1
50-59	4
60-69	8
70-79	14
80-81	10
90-99	3
Jumlah	40

Pembahasan:

Nilai	$f_i$	$x_i$	$f_id_i$	$\mid x_i\bar x\mid$	$f_i\mid x_i - \bar x\mid$	$(x_i - \bar x)^2$
40-49	1	44.5	43.5	29.25	29.25	855.56
50-59	4	54.5	214	19.25	77	370.56
60-69	8	64.5	508	9.25	74	85.56
70-79	14	74.5	1029	0.75	10.5	0.56
80-81	10	84.5	835	10.75	107.5	115.56
90-99	3	94.5	280.5	20.75	62.25	430.56
JUMLAH	40		2910		360.5