Integral Tentu & Penggunaan Integral

Integral Tentu

Catatan: Materi ini merupakan lanjutan dari materi dasar: Pengertian Integral, Integral Tak Tentu & Integral Trigonometri.

Luas suatu bidang dengan bentuk  tertentu (seperti: lingkaran, segitiga, segiempat, dll) dapat ditentukan dengan rumus-rumus dasar yang sudah diketahui. Namun, untuk menentukan luas suatu bidang yang tidak beraturan atau tidak tentu akan sulit. Lihatlah gambar di bawah yang merupakan luasan area dibawah grafik y = f(x) yang dibatasi oleh x = a, x = b, dan garis x. Luas area tersebut hampir mendekati dengan luas dari total 11 segi panjang.

integral tentu menghitung luas kurva

Lihat juga materi StudioBelajar.com lainnya:
Grafik Fungsi Trigonometri
Kuartil & Simpangan Baku

Jika jumlah segi panjang diperbanyak 21 buah seperti gambar dibawah, maka jumlah total luas persegi panjang tersebut semakin mendekati luas area grafik yang ditentukan. Sehingga untuk mendapatkan luas area tersebut, jumlah persegi panjang dibuat mendekati tak hingga. Dapat disimpulkan luas dari area sama dengan limit luas total segi panjang menuju tak hingga.

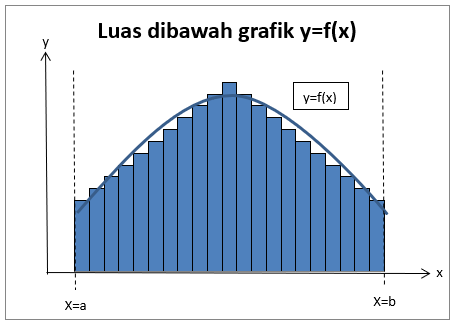
luas bidang di bawah grafik fx

 

Konsep ini menjadi dasar untuk mencari luas suatu bidang tak tentu. Luas suatu bidang di bawah grafik y = f(x) yang dibatasi oleh x = a, x = b dapat dicari dengan mengintegralkan fungsi tersebut pada selang a \le x \le b. Atau dapat ditulis:

Luas =\int^b_af(x)dx

Pengoperasian integral tentu sama dengan intergral tak tentu hanya saja nilai a dan b disubstitusikan dalam fungsi hasil integral sebagai berikut:

\int^b_af(x) dx = [F(x)]^b_a=F(b)-F(a)

Lihat contoh berikut ini sebagai pemahaman:

  • \int^3_1 4x^3dx=[x^4]^3_1=(3^4)-(1^4) = 80
  • \int^2_1\frac{1}{x^3}dx =[-\frac{1}{2x^2}]^2_1 = [-\frac{1}{2(2)^2}]^2_1-(-\frac{1}{2(1)^2}) = -\frac{1}{8}+\frac{1}{2}=\frac{3}{8}

Intergral tentu memiliki sejumlah sifat-sifat penting yang dapat digunakan dalam pengoperasian matematika yaitu:

  • \int^a_a f(x)dx=0
  • \int^b_a f(x) dx = - \int^a_b f(x) dx
  • \int^b_a k \cdot f(x)dx=k \cdot \int^b_af(x)dx     …     dengan k adalah konstanta/ bilangan
  • \int^b_af(x)+g(x)dx = \int ^b_a f(x)dx +\int^b_a g(x)dx
  • \int^b_af(x)-g(x)dx = \int^b_af(x)dx - \int^b_ag(x)dx
  • \int^c_af(x)dx = \int^b_af(x)dx+\int^c_bf(x)dx     …     dengan a < b < c

Pengintegralan suatu fungsi tidak selamanya dapat dikerjakan secara langsung dengan rumus dasar:

\int ax^ndx=\frac{a}{(n+1)}x^{(n+1)}+C

Bisa atau tidak ditentukan oleh bentuk fungsi yang diintegralkan. Teknik pengintegralan terdiri dari dua jenis yaitu teknik substitusi dan teknik parsial.

Lihat juga materi StudioBelajar.com lainnya:
Teks Editorial
Bioteknologi
Conditional Sentence

Penggunaan Integral

Pada penjelasan sebelumnya integral dapat digunakan untuk mencari luas suatu bidang sebagai fungsi pada interval a \le x \le b dan dibatasi sumbu x sebagaimana proses integral tentu. Lihat tabel berikut:

 

Jenis Kegunaan Batasan Luas (A) Keterangan
Luas grafik
  •  Grafik f(x)
  •  a ≤ x ≤ b
  •  Sumbu x
 A =\int^b_a f(x) dx Luas bidang berada pada:

  • Atas sumbu x, atau
  • Bawah sumbu x
Luas antara dua grafik
  •  Grafik f(x)
  •  Grafik g(x)
  •  a ≤ x ≤ b
 A =\int^b_a f(x) - g(x) dx f(x) > g(x) pada selang a ≤ x ≤ b
Luas antara dua grafik dengan ordo maksimal 2
  •  Grafik f(x)
  •  Grafik g(x)
 A = \frac{D \sqrt{D}}{6a^2} Determinan (D) didapat dari f(x) = g(x) menjadi ax2 + bx + c = 0

Pada penggunaan lebih lanjut, integral dapat digunakan untuk mencari volume. Volume didapat dari suatu bidang yang mengelilingi/berputar pada suatu sumbu. Metode untuk menghitung volume benda putar adalah metode cakram dan metode kulit.

Metode Cakram

Jenis Volume Batasan Bidang Sumbu Putar Volume
Volume Grafik
  •  Grafik f(x)
  •  a ≤ x ≤ b
  •  Sumbu x
 Sumbu x V = \int^b_a \pi [f(x)]^2) dx
  •  Grafik f(y)
  •  a ≤ y ≤ b
  •  Sumbu y
 Sumbu y V = \int^b_a \pi [f(y)]^2) dy
Volume Antara Dua Grafik
  •  Grafik f(x)
  •  Grafik g(x)
  •  a ≤ x ≤ b
 Sumbu x V = \int^b_a [f(x)]^2 - [g(x)]^2) dx
  •  Grafik f(y)
  •  Grafik g(y)
  •  a ≤ y ≤ b
 Sumbu y V = \int^b_a [f(y)]^2 - [g(y)]^2) dy
Lihat juga materi StudioBelajar.com lainnya:
Efek Fotolistrik
Reaksi Redoks
Gurindam

Metode Kulit

Jenis Volume Batasan Bidang Sumbu Putar Volume
Volume Grafik
  •  Grafik f(x)
  •  a ≤ x ≤ b
  •  Sumbu x
 Sumbu y V = 2 \pi \int^b_a x \cdot f(x) dx
Volume Antara Dua Grafik
  •  Grafik f(x)
  •  Grafik g(x)
  •  a ≤ x ≤ b
 Sumbu y V = 2 \pi \int^b_a x \cdot [f(x) - g(x)] dx

Contoh Soal Integral Tentu, Penggunaan Integral, dan Pembahasan

Tentukan luas daerah yang dibatasi oleh 2 grafik yaitu grafik y = 2x^3 + x^2 - x - 1 dan grafik y = x^3 + 2x^2 - x - 1.

Pembahasan:

Kedua grafik dibuat persamaan f(x) – g(x) untuk mendapat titik potong:

2x^3 + x^2 - x - 1 = x^3 + 2x^2 + 5x  - 1

x^3 - x^2 - 6x = 0

(x+2)(x)(x-3) = 0

Akar-akarnya merupakan titik potong kedua grafik yaitu x = -2, x = 0, x = 3.

Maka luas grafik tersebut adalah:

A =\int^b_a f(x) - g(x) dx = \int^c_a f(x) - g(x) dx + \int^b_c f(x) - g(x) dx

Dengan a = -2, b = 3, dan c = 0, maka

A =\int^0_{-2} f(x) - g(x) dx = \int^0_{-2} x^3 - x^2 - 6x dx = [\frac{1}{4}x^4 - \frac{1}{3}x^3 - \frac{6}{2}x^2]^0_{-2}

= 0 - (\frac{1}{4}(-2)^4 - \frac{1}{3}(-2)^3 - \frac{6}{2}(-2)^2)

= 0 - (\frac{16}{4} - \frac{8}{3} - 12) = - (\frac{48 + 32 - 144}{12}) = \frac{64}{12}

A =\int^3_0 f(x) - g(x) dx = \int^3_0 x^3 - x^2 - 6x dx = [\frac{1}{4}x^4 - \frac{1}{3}x^3 - \frac{6}{2}x^2]^3_0

= (\frac{1}{4}(3)^4 - \frac{1}{3}(3)^3 - \frac{6}{2}(3)^2) - 0 = \frac{81}{4} - 9 - 27 = - \frac{63}{4}

Nilai - \frac{63}{4} memiliki tanda (-) mengartikan pada interval 0 ≤ x ≤ 3 kurva g(x) > f(x), sehingga penulisan integran terbalik. Seharusnya: g(x) – f(x). Luas tidak mungkin (-) sehingga yang dijumlahkan adalah \frac{63}{4}. Sebagai berikut:

A = \int^c_a f(x) - g(x) dx + \int^b_c f(x) - g(x) dx = \frac{64}{12} + \frac{63}{4} = \frac{64 + 189}{12} = \frac{253}{12} = 21 \frac{1}{12}

Artikel: Integral Tentu dan Penggunaan Integral
Kontributor: Alwin Mulyanto, S.T.
Alumni Teknik Sipil FT UI

Materi StudioBelajar.com lainnya:

  1. Logaritma
  2. Logika Matematika
  3. Deret Geometri Tak Hingga