Pertidaksamaan
Pertidaksamaan adalah suatu kalimat matematika yang mengandung notasi lebih kecil dari (<), lebih besar dari (>), lebih kecil dari atau sama dengan , dan notasi lebih besar dari atau sama dengan
. Penyelesaian dari pertidaksamaan membuat kalimat matematikanya menjadi benar.
Pertidaksamaan Linier
Pertidaksamaan linier merupakan bentuk pertidaksamaan yang memuat bentuk aljabar dengan ordo satu misal atau
. Dalam penyelesaian petidaksamaan terdapat beberapa sifat-sifat pertidaksamaan yang perlu diketahui. Sifat-sifat ini berlaku untuk semua jenis pertidaksaman (linier, kuadrat, pecahan, dll) yaitu:
- Suatu pertidaksamaan dapat ditambah atau dikurang oleh suatu bilangan maupun bentuk aljabar. Penambahan tidak mempengaruhi nilai atau tanda pertidaksamaan asalkan kedua ruas sama-sama ditambah atau dikurangi.
Contoh:
Jika, maka
- Suatu pertidaksamaan dapat dikalikan dengan suatu bilang. Notasi pertidaksamaan tergantung pada nilai dari bilangan pengalinya. Jika bilangan pengalinya lebih besar dari nol, notasi tidak berubah. Namun, jika lebih kecil dari nol, notasi berubah/ dibalik.
Contoh:
– Jikadan
, maka
– Jikadan
, maka
- Suatu pertidaksamaan dapat dipangkatkan, namun notasi pertidaksamaan bisa saja berubah tergantung dari hasil pangkat masing-masing ruas.
Contoh:
– Jika,
, dan
, maka
, tetapi
- Dua pertidaksamaan dapat digabungkan dengan menambahkan kata “atau” dan “dan” dalam kalimat matematikanya. Kata “atau” jika kedua pertidaksamaan memiliki daerah penyelesaian yang saling lepas.
Penyelesaian ini dapat mengunakan garis bilangan.
Contoh :atau
Kata “dan” jika kedua pertidaksamaan memiliki daerah penyelesaian yang terikat dan membentuk interval.
Contoh :dan
, sehingga dalam garis bilangan membentuk interval
- Jika dua aljabar dikalikan dalam suatu pertidaksamaan berlaku:
- Jika
maka a dan b bertanda sama yaitu :
dan
atau
dan
- Jika
maka a dan b berlainan tanda yaitu :
dan
atau
dan
Misalkan, maka:
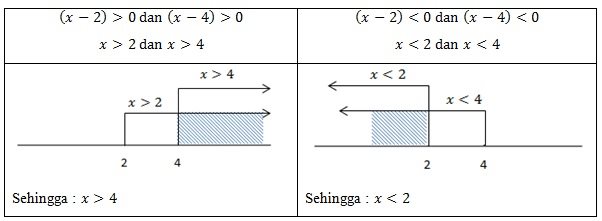 Jadi penyelesaiannya adalah
Jadi penyelesaiannya adalah dan
- Jika
- Dua bentuk pertidaksamaan dapat dijumlahkan dengan catatan memiliki notasi pertidaksamaan yang sama.
Contoh:
Irisan Kerucut
Persamaan & Pertidaksamaan Logaritma
Vektor
Pertidaksamaan Kuadrat
Pertidaksamaan kuadrat merupakan bentuk pertidaksamaan yang memuat bentuk aljabar dengan ordo maksimal dua misal dengan notasi bisa berupa yang lain (
). Dalam penyelesaiannya, nilai yang memenuhi petidaksamaan kuadrat disebut penyelesaian. Penyelesaian dapat dicari dengan garis bilangan. Berikut langkah-langkahnya:
- Menentukan akar-akar dari persamaan
- Akar-akar ditempatkan pada garis bilangan sebagai batas interval.
- Substitusi sembarang nilai yang ada di setiap interval pada
- Tempatkan tandan (+) atau (-) pada setiap interval sesuai dengan hasil substitusi sebelumnya.
- Didapatkan interval yang menjadi penyelesaian yaitu yang bertanda (+) untuk penyelesaian pertidaksamaan
dan yang bertanda (-) untuk penyelesaian pertidaksamaan
Dalam permasalahan persamaan kuadrat, diskriminan (D) bisa digunakan untuk mendapatkan penyelesaian dalam bentuk pertidaksamaan. Contoh : Tentukan nilai p agar persamaan memiliki akar-akar yang real dan bebeda. Maka:

Pertidaksamaan Pecahan
Pertidaksamaan pecahanan terdiri dari fungsi dan
. Secara umum, bentuk pertidaksamaannya dapat dinyatakan dengan :
dengan notasi (>) bisa sebagai :
atau
Penyelesaian pertidaksamaan pecahanan dapat dilakukan dengan langkah:
- Menentukan akar dari
dan
- Selanjutnya sama dengan pertidaksamaan kuadrat.
- Menetapkan penyelesaian dengan:
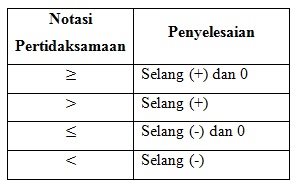
Pertidaksamaan Irasional
Pertidaksamaan yang mengandung bentuk akar disebut sebagai pertidaksamaan irasional. Bentuk-bentuk:
Dapat dikerjakan dengan mengkuadratkan kedua ruas. Namun ada syarat yang perlu ditambahkan jika dikuadatkan yaitu:
dan
Penyelesaian pertidaksamaan irasional dapat dilakukan dengan langkah-langkah sesuai dengan pertidaksamaan kuadrat.
Pertidaksamaan Nilai Mutlak
Nilai mutlak dari suatu bilangan adalah nilai positif dari bilangan tersebut. Misalkan nilai mutlak dari 5 adalah 5 dan nilai mutlak dari -5 adalah 5 . Nilai mutlak dinotasikan dengan “
“, contoh :
. Nilai mutlak juga bisa berupa persamaan atau pertidaksamaan.
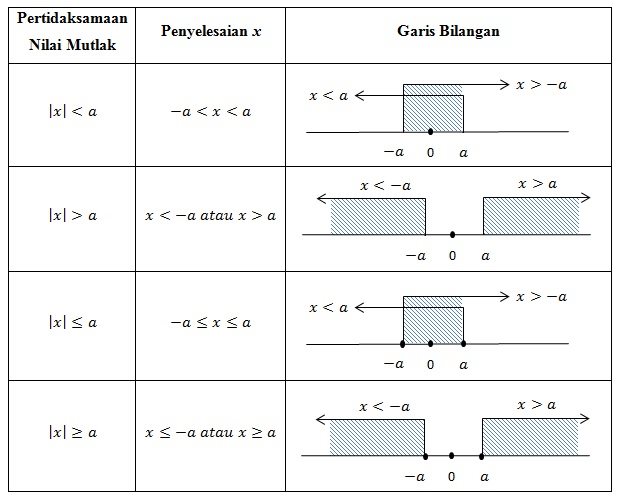
Jika artinya nilai mutlak yang memenuhi antara 0 sampai 2 karena nilai mutlak selalu positif. Dengan nilai mutlak tersebut, maka nilai
berada pada
. Tabel diatas juga berlaku jika mencari penyelesaian nilai mutlak dari suatu fungsi dengan cara mengganti variabel sebagai fungsi menjadi
, contoh penyelesaian
adalah:

Jika pertidaksamaan melibatkan 2 nilai mutlak di kedua ruas, maka penyelesaian dengan cara mengkuadratkan kedua ruas sehingga notasi mutlak hilang. Contoh, penyelesaian adalah:

Contoh Soal Pertidaksamaan dan Pembahasan
Contoh Soal 1
Tentukan penyelesaian dari:
Pembahasan 1:
Akar-akarnya:
Garis bilangan adalah:

Penyelesaian :
-5 < x < atau x > 3
Contoh Soal 2
Tentukan penyelesaian dari:
Pembahasan 2:
Akar-akarnya:
dan
Syarat yang harus dipenuhi:
dan
tidak ada karena diskriminan
Garis Bilangannya:
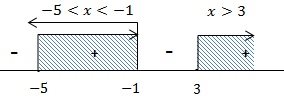
Penyelesaian:
-5 < x < -1 atau x > 3
Contoh Soal 3
Tentukan penyelesaian dari:
Pembahasan 3:
Misalkan ,
maka:
Nilai mutlak:
Sehingga:
, selalu benar untuk nilai x real
Penyelesaian:
0 < x < 6
Artikel: Irisan Kerucut
Kontributor: Alwin Mulyanto, S.T.
Alumni Teknik Sipil FT UI
Materi StudioBelajar.com lainnya:
- Fungsi Komposisi dan Fungsi Invers
- Sudut Istimewa Trigonometri
- Perkalian, Determinan, & Invers Matriks
Pertidaksamaan adalah suatu kalimat matematika yang mengandung notasi lebih kecil dari (<), lebih besar dari (>), lebih kecil dari atau sama dengan , dan notasi lebih besar dari atau sama dengan
. Penyelesaian dari pertidaksamaan membuat kalimat matematikanya menjadi benar.
Pertidaksamaan Linier
Pertidaksamaan linier merupakan bentuk pertidaksamaan yang memuat bentuk aljabar dengan ordo satu misal atau
. Dalam penyelesaian petidaksamaan terdapat beberapa sifat-sifat pertidaksamaan yang perlu diketahui. Sifat-sifat ini berlaku untuk semua jenis pertidaksaman (linier, kuadrat, pecahan, dll) yaitu:
- Suatu pertidaksamaan dapat ditambah atau dikurang oleh suatu bilangan maupun bentuk aljabar. Penambahan tidak mempengaruhi nilai atau tanda pertidaksamaan asalkan kedua ruas sama-sama ditambah atau dikurangi.
Contoh:
Jika, maka
- Suatu pertidaksamaan dapat dikalikan dengan suatu bilang. Notasi pertidaksamaan tergantung pada nilai dari bilangan pengalinya. Jika bilangan pengalinya lebih besar dari nol, notasi tidak berubah. Namun, jika lebih kecil dari nol, notasi berubah/ dibalik.
Contoh:
– Jikadan
, maka
– Jikadan
, maka
- Suatu pertidaksamaan dapat dipangkatkan, namun notasi pertidaksamaan bisa saja berubah tergantung dari hasil pangkat masing-masing ruas.
Contoh:
– Jika,
, dan
, maka
, tetapi
- Dua pertidaksamaan dapat digabungkan dengan menambahkan kata “atau” dan “dan” dalam kalimat matematikanya. Kata “atau” jika kedua pertidaksamaan memiliki daerah penyelesaian yang saling lepas.
Penyelesaian ini dapat mengunakan garis bilangan.
Contoh :atau
Kata “dan” jika kedua pertidaksamaan memiliki daerah penyelesaian yang terikat dan membentuk interval.
Contoh :dan
, sehingga dalam garis bilangan membentuk interval
- Jika dua aljabar dikalikan dalam suatu pertidaksamaan berlaku:
- Jika
maka a dan b bertanda sama yaitu :
dan
atau
dan
- Jika
maka a dan b berlainan tanda yaitu :
dan
atau
dan
Misalkan, maka:
 Jadi penyelesaiannya adalah
Jadi penyelesaiannya adalah dan
- Jika
- Dua bentuk pertidaksamaan dapat dijumlahkan dengan catatan memiliki notasi pertidaksamaan yang sama.
Contoh:
Irisan Kerucut
Persamaan & Pertidaksamaan Logaritma
Vektor
Pertidaksamaan Kuadrat
Pertidaksamaan kuadrat merupakan bentuk pertidaksamaan yang memuat bentuk aljabar dengan ordo maksimal dua misal dengan notasi bisa berupa yang lain (
). Dalam penyelesaiannya, nilai yang memenuhi petidaksamaan kuadrat disebut penyelesaian. Penyelesaian dapat dicari dengan garis bilangan. Berikut langkah-langkahnya:
- Menentukan akar-akar dari persamaan
- Akar-akar ditempatkan pada garis bilangan sebagai batas interval.
- Substitusi sembarang nilai yang ada di setiap interval pada
- Tempatkan tandan (+) atau (-) pada setiap interval sesuai dengan hasil substitusi sebelumnya.
- Didapatkan interval yang menjadi penyelesaian yaitu yang bertanda (+) untuk penyelesaian pertidaksamaan
dan yang bertanda (-) untuk penyelesaian pertidaksamaan
Dalam permasalahan persamaan kuadrat, diskriminan (D) bisa digunakan untuk mendapatkan penyelesaian dalam bentuk pertidaksamaan. Contoh : Tentukan nilai p agar persamaan memiliki akar-akar yang real dan bebeda. Maka:

Pertidaksamaan Pecahan
Pertidaksamaan pecahanan terdiri dari fungsi dan
. Secara umum, bentuk pertidaksamaannya dapat dinyatakan dengan :
dengan notasi (>) bisa sebagai :
atau
Penyelesaian pertidaksamaan pecahanan dapat dilakukan dengan langkah:
- Menentukan akar dari
dan
- Selanjutnya sama dengan pertidaksamaan kuadrat.
- Menetapkan penyelesaian dengan:

Pertidaksamaan Irasional
Pertidaksamaan yang mengandung bentuk akar disebut sebagai pertidaksamaan irasional. Bentuk-bentuk:
Dapat dikerjakan dengan mengkuadratkan kedua ruas. Namun ada syarat yang perlu ditambahkan jika dikuadatkan yaitu:
dan
Penyelesaian pertidaksamaan irasional dapat dilakukan dengan langkah-langkah sesuai dengan pertidaksamaan kuadrat.
Pertidaksamaan Nilai Mutlak
Nilai mutlak dari suatu bilangan adalah nilai positif dari bilangan tersebut. Misalkan nilai mutlak dari 5 adalah 5 dan nilai mutlak dari -5 adalah 5 . Nilai mutlak dinotasikan dengan “
“, contoh :
. Nilai mutlak juga bisa berupa persamaan atau pertidaksamaan.

Jika artinya nilai mutlak yang memenuhi antara 0 sampai 2 karena nilai mutlak selalu positif. Dengan nilai mutlak tersebut, maka nilai
berada pada
. Tabel diatas juga berlaku jika mencari penyelesaian nilai mutlak dari suatu fungsi dengan cara mengganti variabel sebagai fungsi menjadi
, contoh penyelesaian
adalah:

Jika pertidaksamaan melibatkan 2 nilai mutlak di kedua ruas, maka penyelesaian dengan cara mengkuadratkan kedua ruas sehingga notasi mutlak hilang. Contoh, penyelesaian adalah:

Contoh Soal Pertidaksamaan dan Pembahasan
Contoh Soal 1
Tentukan penyelesaian dari:
Pembahasan 1:
Akar-akarnya:
Garis bilangan adalah:

Penyelesaian :
-5 < x < atau x > 3
Contoh Soal 2
Tentukan penyelesaian dari:
Pembahasan 2:
Akar-akarnya:
dan
Syarat yang harus dipenuhi:
dan
tidak ada karena diskriminan
Garis Bilangannya:

Penyelesaian:
-5 < x < -1 atau x > 3
Contoh Soal 3
Tentukan penyelesaian dari:
Pembahasan 3:
Misalkan ,
maka:
Nilai mutlak:
Sehingga:
, selalu benar untuk nilai x real
Penyelesaian:
0 < x < 6
Artikel: Irisan Kerucut
Kontributor: Alwin Mulyanto, S.T.
Alumni Teknik Sipil FT UI
Materi StudioBelajar.com lainnya:
- Fungsi Komposisi dan Fungsi Invers
- Sudut Istimewa Trigonometri
- Perkalian, Determinan, & Invers Matriks
